

A circle of confusion (usually written in equations as CoC), is an optical spot, of vaguely circular shape, caused when a cone of light coming from a point source is not brought to a perfect point focus by a lens system. One reason there might be a circle is that the lens just isn't focused. Even when the lens is focused, though, there will always be a circle of confusion of some shape and size. The circle will really be the shape of the opening in the aperture, and additionally, no lens is capable of perfect operation, although modern manufacturers go to extremes to get as close as possible. The best a lens can do is called the circle of least confusion.
The good thing, is that if the circle is small enough, we don't notice it. In fact, that's how depth of field is defined. It's the range of distances for a particular setup of a camera, for which the circle of confusion is too small for us to notice. In a minute we'll talk more about what too small to notice means.
You need to know the CoC for your camera to figure out the Depth of Field for a given focal length, aperture, sensor size combination. Further, if you understand about CoC, you'll also understand how to use your camera better.
Look at the diagram to the left. I wish I would have had something like it when I first started learning about depth of field and circle of confusion. Take a few minutes to play with the controls. In particular, open up the aperture, put the image out of focus and see the size of the circle. Then shut the aperture down. Immediately you'll see why a small aperture, (big numbers), makes for greater depth of field (more stuff in focus at different distances). With a small aperture, something that makes a BIG circle of confusion with a large aperture, will make a small circle of confusion barely bigger than an in-focus image.
We said that the definition of depth of field is: the range of distances, for a particular setup of a camera, for which the circle of confusion is too small for us to notice. Well, that depends on how we look. We're going to make a photo of some size, and we're going to look at that photo from some distance. Additionally, to make that photo, we have to enlarge the information from the camera's sensor. A smaller sensor will need to be enlarged more than a large sensor, so the smaller sensor has to have a smaller CoC so that after more enlargement the viewer can't detect the difference between a circle of confusion and a point. Each of these can affect our definition of CoC. If we blow the photo up to six foot across, lay it on the floor and crawl around on it looking with a magnifying glass, we'll see some pretty small flaws. If we make the photo 6"x4" and look at it by two feet away, we won't notice much at all.

Most people don't like to look at things closer than about 25 cm (about 10 in) away, and when viewing photos we like to see about 60°. If we're looking at something about 25 cm away and it covers about 60° that makes it about 10" tall, so imagine we're looking at an 8"X10" photograph.

At this distance, if you have good vision, you should be able to resolve (tell apart) about 5 line pairs per millimeter (lp/mm). A millimeter is just over one thirty-second of an inch. A line pair is a dark line and an adjacent light line. So if we can determine 5 line pairs per millimeter, that means that we need to have a line every fifth of a millimeter (0.2 mm). That means, that at full size, our circle of confusion is 0.2 mm. If it's bigger than that, we'll notice it, and remember that's our definition of circle of confusion, it's the biggest thing that still looks like a point. If it's bigger than 0.2 mm, then we'll find ourselves peering at the picture trying to bring it into focus but it just won't quite, it will look blurry. We'll notice the lack of detail.
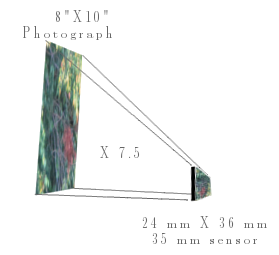
We want the image to look clear at 8"X10" when it's 10" or so away, so it needs a CoC of 0.2 mm. The sensor or film that recorded it, though, was probably much smaller. We want it to record well enough so that when the image is blown up, or enlarged to 8"X10", the CoC is 0.2 mm, which means that the original on the sensor has to be much smaller. The 35 mm sensor has a diagonal of about 43 mm, and an 8"X10" photograph has a diagonal of just over 325 mm. That's a multiple of 7.5. So if we want our circle of confusion to scale up by 7.5 to 0.2 mm, that means it has to be 0.2 mm/7.5, or about 0.027 mm. A common convention in the photo industry is to use 0.03 mm for the CoC when doing Depth of Focus calculations. Using 0.027 mm is just a tiny bit pickier about what's in focus and what's not.
It couldn't be simpler. You'll need to know your cropping multiplier, (also sometimes called the focal length multipler), or you'll need to know your sensor size.
TOTAL_MULTIPLIER = 7.5 X CROPPING_MULTIPLIER
CoC = 0.2 mm / TOTAL_MULTIPLIER
First multiply 7.5 (the amount a 35 mm sensor has to be blown up to get to 8"X10"), times your cropping multiplier. The result tells you how much you have to multiply your sensor image by to be as big as an 8"X10" picture. Now, divide the 0.2 mm desired final CoC by whatever you got. For example, my Canon SX20IS point and shoot has a multiplier of 5.6. That means my sensor is tiny compared to a 35 mm sensor. You have to scale mine up by 5.6 just to get up to the size of a 35 mm sensor. Now, multiplying that by 7.5 that gives me about 42. That means an image on my sensor has to be scaled up 42 times to be as big as an 8"X10" photograph. That means, that any fuzzyness has to be scaled up 42 times as well, and if I want the final CoC to be 0.2 mm, on my sensor, it had better be 0.2 mm/42, or about .0047 mm. (And it does just fine, each pixel on the thing is only .0015 mm X .00147 mm!)
DIAGONAL = √(LENGTH²+WIDTH²)
TOTAL_MULTIPLIER=325.28 mm / DIAGONAL
CoC = 0.2 mm / TOTAL_MULTIPLIER
Fine. Couldn't be easier. We know the diagonal of an 8"X10" photograph, in millimeters, is 325.28 mm. We just need to know the diagonal of your sensor to get the multiplier, just like we did for the 35 mm sensor.
We'll use the Pythagorean theorem which tells us that the length of the diagonal of a rectangle is the square root of the sum of the squares of the sides. √(x²+y²).
You can use a calculator, or use the tool I made for you right below this. So, once you have your diagonal, divide it into the 8"X10" photo's diagonal, (325.28mm), to get the CoC multiplier.
Divide the 8"X10" photo's CoC (0.2 mm) by the multiplier you came up with and that will give you the one you need for your sensor when doing Depth of Field calculations.
As an example, my Canon SX20IS has a sensor that measures about 6.17 mm X 4.5 mm. Plugging that into Pythagorean's theorem, we get √(6.17²+4.5²) which comes out to about 7.666. That tells me that my sensor measures about 7.666 mm diagonally.
Now we take the 8"X10" photo's diagonal and divide it by the sensor's diagonal. 325.28 mm/7.666 mm is about 42.43.
Dividing the 8"X10" photo's CoC by that: 0.2mm/42.43 = 0.0047 mm, the same CoC we came up with the other method.